[TA] #4 밀집 표현(dense representation)을 만들자! 워드 임베딩 - Word2Vec

 

 

* This content is based on the article written by Ji Ho Park and Gichang Lee

* This content is based on the lecture content of Prof. Pilsung Kang

---

요약

1. 단순 빈도(frequency)에 기반한 국소 표현은 희소 표현(sparse representation)이기 때문에 차원의 저주(curse of dimensionality)라는 문제 발생
2. 단어장 크기보다 적은 차원의 밀집 표현(dense representation)을 만들어 저차원에 축소해 보자는 아이디어 
3. 단어 간의 의미 관계를 포착하여 단어 벡터를 학습하는 워드 임베딩: Word2Vec, GloVe, FastText

 

본 포스팅에서는 단어를 벡터화하는 임베딩(embedding) 방법론 중 Word2Vec에 대해 자세히 알아보고자 합니다. 

---

워드 임베딩(Word Embedding)이란?

Word2Vec의 내용으로 들어가기 전에 워드 임베딩이 무슨 의미인지 확인해 보겠습니다. 

• 일반적 의미:

"embed"의 기본 동사형에서 파생된 "embedding"은 무엇인가를 삽입하거나, 고정시키는 것을 의미합니다. 

• 개념적 의미:

개념이나 아이디어를 더 큰 맥락이나 구조에 포함시키는 것을 의미합니다. 

• 컴퓨터 과학/수학적 의미:

어떤 수학적 공간이나 구조를 다른 공간으로 변환하거나 매핑하는 것을 의미합니다. 

 

위 내용을 바탕으로 워드 임베딩의 맥락에서의 의미는 다음과 같습니다. 

단어를 벡터 공간에 매핑하여 단어 간의 의미적 관계를 숫자 벡터 형태로 표현하는 것

• 단어를 n차원 벡터로 "삽입"한다는 개념에서 비롯된 용어이며, 
• 이 과정은 단어의 의미를 수학적으로 고정시키고, 단어 간의 유사성을 파악할 수 있도록 합니다.

지난 포스팅들에서 우리는 단어를 어떻게 표현할 수 있는지 그리고 단어들 간의 유사성을 어떻게 측정할 수 있는지 배웠습니다. 원-핫 벡터는 단어를 \(N × 1\) 열 벡터로 표현합니다. 분석하고자 하는 문서 집합 즉 코퍼스가 클수록 단어의 개수가 몇 천, 몇 만으로 커질 수 있습니다. 그리고 단어를 표기하는 1개의 행 이외에는 모두 0으로 채워져 있기 때문에 매우 듬성듬성(sparse)한 행렬이 생성됩니다. 이러한 경우 연산에 매우 비효율적이며 벡터들 간의 유사성을 측정하는 것이 불가능합니다. 임베딩은 더 적은 숫자들로 하나의 단어에 대한 정보를 담아 워드 벡터로 표현하여 하나의 단어를 몇 천 차원, 몇 만 차원이 아닌 몇십, 몇 백 차원으로 낮추려는 게 목표입니다. 이를 통해 빽빽(dense)한 행렬을 만들어 단어 간의 유사성을 파악할 수 있도록 하며, 계산 효율성을 높일 수 있습니다. 워드 임베딩의 모든 행은 0이 아닌 어떠한 숫자로 채워지기 때문입니다.

Sparse and Dense vector comparison (source: Pinecone)

즉 단어 임베딩(Word Embedding)은 단어를 문서 내 단어의 개수 \(|V|\) 보다 훨씬 적은 숫자인 \(n\) 차원의 벡터로 축소하여 성분이 0 혹은 1이 아닌 연속적인 숫자로 구성되게 합니다. 그렇기 때문에 단어 벡터끼리 내적 하여도 0이 아니게 되며 단어 간의 의미(semantic) 관계가 보존됩니다. 아래 그림은 임베딩을 통해 추출해 낸 단어 벡터 간의 관계를 시각화한 것입니다.

<왕> - <남자> + <여자> = ? 

<마드리드> - <스페인> + <프랑스> = ?

 

우리는 언어 상식을 이용하면 위 문제에 대한 답을 충분히 유추해 낼 수 있습니다. 우리는 각 단어 간의 관계를 여태까지 읽어온 수많은 글을 통해 이미 머릿속에 구축해 왔기 때문입니다. 

word-based arithmetic (source: Medium)

기계는 특정 단어에 대한 의미를 주변 단어 들에 의해서 정의합니다. 이를 분포 의미론(Distributional Hypothesis)이라고 첫 시간에 이야기했습니다. 그럼 워드 임베딩과 분포 의미론의 관계를 다시 살펴보겠습니다. 

 

워드 임베딩과 분포 의미론(Distributional Hypothesis)

워드 임베딩은 분포 의미론에 기반하는데 Distributional semantics에 대해서 먼저 이해할 필요가 있습니다. 

Distributional semantics: 대량의 언어 데이터의 분포적인 성질에 기반하여 언어적 요소 간의 의미적 유사성을 수량화하는 방법을 개발하는 연구 분야를 의미

분포 의미론은 같은 맥락(context)에서 사용된 단어들은 유사한 의미를 나타내는 경향을 보인다는 것입니다. 예를 들어 '강아지'라는 단어는 '귀엽다', '예쁘다', '애교' 등의 단어와 같이 자주 등장한다고 해봅시다. 그에 따라 분포 의미론에 맞춰 해당 단어들을 벡터화한다면 유사한 값이 나올 것이고 의미적으로 가까운 단어가 된다는 뜻입니다. 이러한 아이디어에 착안하여 비슷한 컨텍스트를 공유하는 단어는 다차원의 벡터 의미 공간 안에서 비슷한 위치에 표현하도록 하는 것이 워드 임베딩의 핵심입니다. 즉 유사한 단어는 유사한 임베딩 벡터를 지닌다는 의미이기도 합니다. 그렇기 때문에 벡터 의미 공간 속에서 단어 간 의미적 유사도를 측정하게 되면 두 개의 유사한 단어는 임베딩 벡터의 내적 값이 상당히 높게 산출됩니다. 이쯤에서 지난 포스팅에서 학습한 코사인 유사도를 다시 한번 생각해 봅시다. 

Cosine Similarity (source: learndatasci)

지난 포스팅에서 다룬 수식에 따라 코사인 유사도는 -1에서 1 사이의 값을 가지며 두 임베딩 벡터를 x, y 각각의 단어라고 생각한다면, 이는 곧 두 단어 간의 의미적 유사도가 됩니다.

• 코사인 유사도가 -1에 가깝다면 두 임베딩 벡터는 다른 방향의 벡터라는 것을 의미하고, 이는 두 단어가 의미적으로 반대임을 알 수 있습니다. 
• 코사인 유사도가 0일 때는 두 임베딩 벡터가 직교(orthogonal)하는 경우로 이는 두 단어 간에 관련이 없음을 의미합니다. 
• 코사인 유사도가 1에 가깝다면 두 단어는 동일한 방향의 임베딩 벡터이고 의미적으로 유사함을 나타냅니다. 

이번 포스팅에서는 지난 2013년 구글의 토마스 미콜로프가 이끄는 연구팀에서 발표한 Word2Vec을 통해 워드 임베딩의 원리에 대해 알아보고자 합니다. 이 방법을 확장하면 Doc2Vec, Sentence2Vec, Graph2Vec, Item2Vec 등 '2Vec' 방법론에 대한 이해도를 높일 수 있는 아주 좋은 첫 주제입니다. 

 

Word2Vec 개요

Word2Vec은 크게 CBoW (Continuous Bag of Words)와 Skip-Gram 두 가지 방식이 있습니다. 전자는 주변에 있는 단어들을 가지고 중심에 있는 단어를 예측하는 방식이고, 후자는 반대로 중심에 있는 단어로 주변 단어를 예측하는 방식입니다. 다음의 사례를 통해 그 차이를 확인해 보겠습니다. 

(1) CBoW: 주변 단어들을 모두 합쳐서 본 후 타겟 단어를 맞추기
(2) Skip-Gram: 타겟 단어를 보고 주변 단어들을 맞추기

위 그림에서 "fox"가 target이라면, CBoW의 경우 주변 단어인 ["The", "quick", "brown", "jumps", "over"]을 가지고 중심에 있는 "fox"을 예측하려 한다면, Skip-Gram의 경우 ["fox"]을 가지고 주변 단어인 "The", "quick", "brown", "jumps", "over"를 각각 예측하려는 것입니다. 예측을 위한 Classification model은 neural network로 구현이 되고, stochastic gradient descent (SGD)로 학습이 수행됩니다. input은 \(N×1\) word embedding vector로 들어갑니다. 처음에는 무작위의 숫자로 초기화되지만, 학습이 진행될수록 word embedding vector는 주변 단어들과의 의미적 관계 정보가 encoding 되어 업데이트됩니다. 자세한 학습 원리와 절차는 다음 포스팅에서 설명하겠습니다. 얼핏 생각해 보면 더 많은 정보를 받아서 단어를 예측하는 CBoW의 성능이 좋을 것으로 생각하기 쉽지만, 실제로는 Skip-Gram이 역전파를 통해 더 많은 학습 정보를 받을 수 있습니다. 아래는 학습이 되는 과정을 도식화한 이미지입니다. 이를 바탕으로 그 이유를 설명해 보겠습니다. 

The CBoW approach in Word2Vec (source: pinecone)

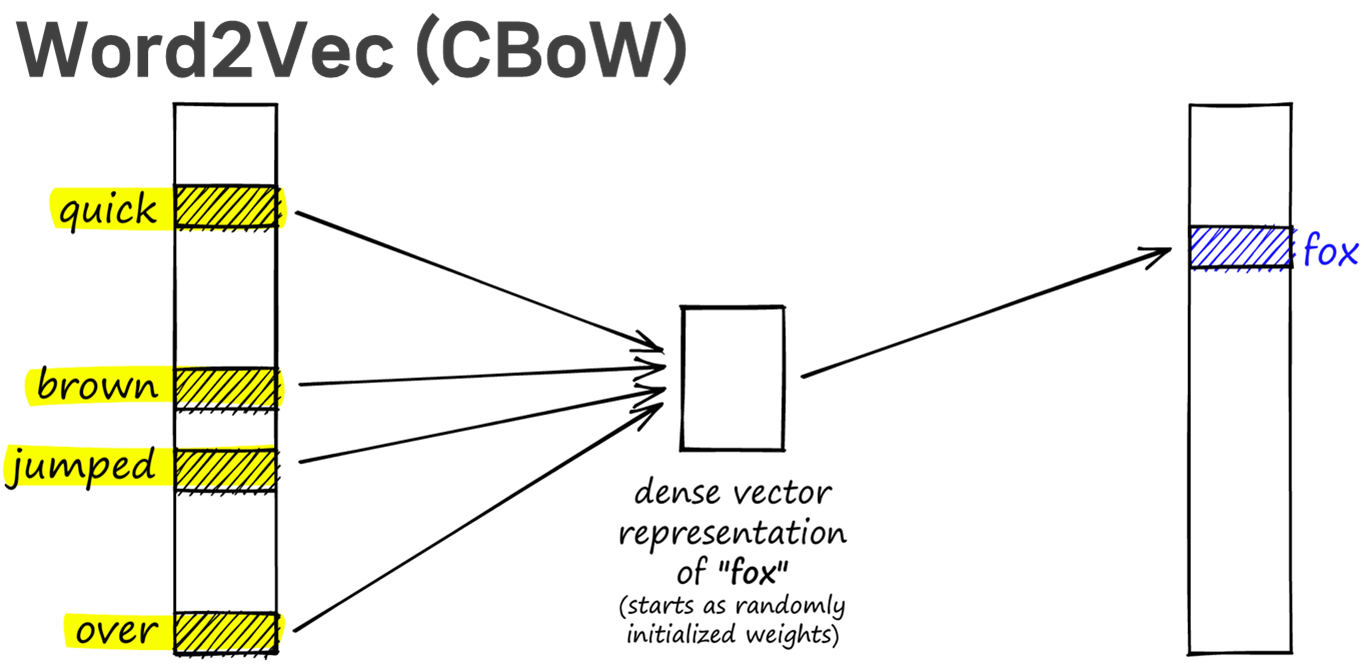
역전파의 관점에서 생각해 보면, CBoW는 타겟 단어 "fox"의 학습 정보를 주변 단어 "quick", "brown", "jumped", "over" 4개가 모두 나누어 받게 됩니다. 한 명의 선생님이 4명의 학생에게 학습 정보를 나누어주는 셈입니다. 

The Skip-Gram approach in Word2Vec (source: pinecone)

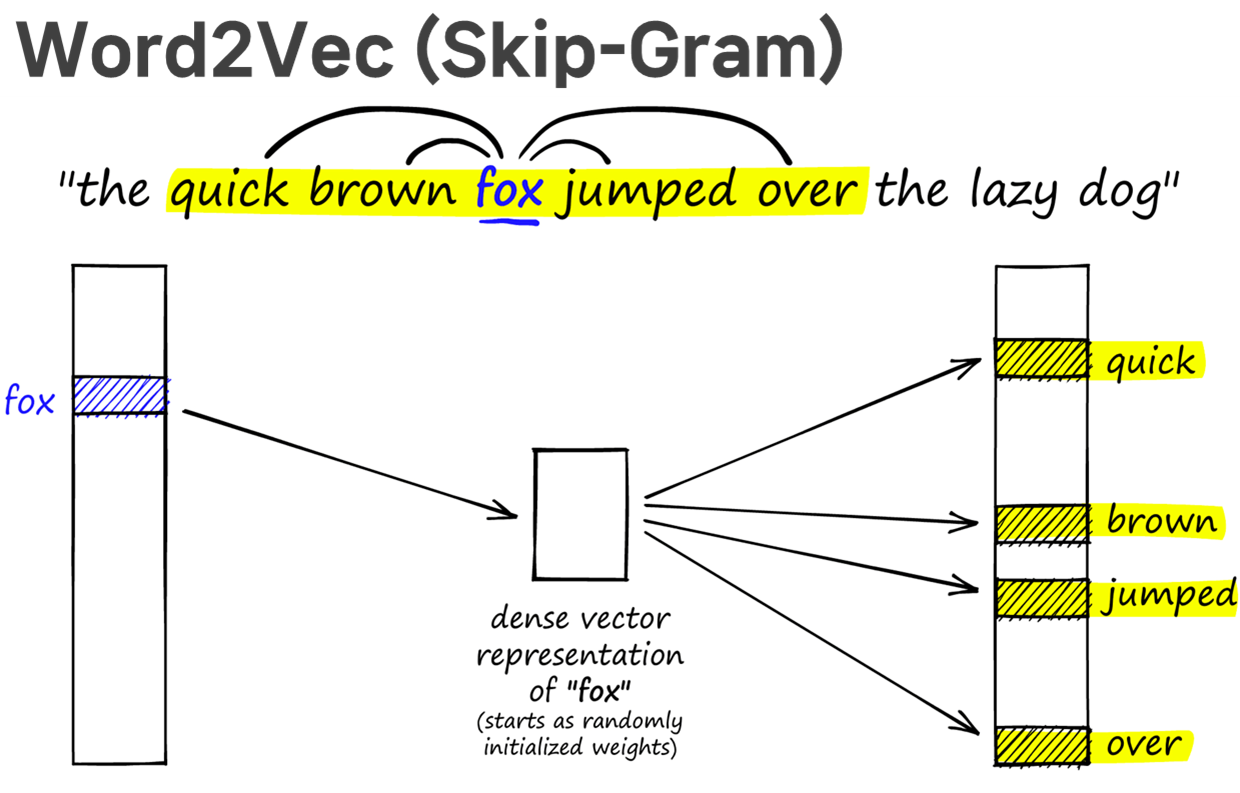
한편 Skip-Gram은 주변 단어 "quick", "brown", "jumped", "over" 4개의 학습 정보를 타겟 단어 "fox"가 단독으로 받게 됩니다. 한 명의 학생을 위해 4명의 선생님이 학습 정보를 제공한 셈입니다. 실험적으로 Skip-Gram이 CBoW보다 성능이 더 좋지만 하나의 타겟 단어를 학습하는 데 더 많은 학습 정보를 요구하므로 (1) 시간이 더 오래 소요되고 (2) 더 많은 컴퓨팅 자원을 필요로 한다는 단점이 있습니다. 이러한 단점에도 불구하고 실제로는 모델의 성능 덕분에 CBoW보다는 Skip-Gram이 더 많이 사용됩니다. 그렇기 때문에 본 포스팅에서는 Skip-Gram을 중심으로 핵심 개념을 살펴보겠습니다. 

 

Word2Vec: softmax regression의 확장판

Softmax regression은 데이터 \((X, Y)\)를 이용하여, 입력된 input \(x\)가 클래스 \(y\)가 될 확률을 최대화시키는 방향으로 클래스 \(y\)의 대표벡터를 coefficient \(\beta\)에 학습합니다. 

$$maximize P(y_{k}|x)=\frac{exp(\beta_{yk}^{T}x)}{\sum_{j}exp(\beta_{j}^{T}x)}$$

위 수식을 살펴보면, \(x\)에 대한 \(y\)의 확률은 \(x\)와 모든 클래스 종류의 \(y_{j}\)와의 내적을 exponential 함수에 넣어 non-negative로 만든 뒤, 모든 \(exp(\beta_{j}^{T}x)\)의 합으로 나누어 확률 형태를 만듭니다. \(x\)가 입력되었을 때 \(y\)가 가장 큰 확률을 가지기 위해서는 어떻게 되어야 할까요? 해당 \(y\)와 \(x\)의 내적값은 가장 크고, 이외에 다른 \(y_{j}\)와 \(x\)의 내적값은 작아야 합니다. 즉 \(x\)와 이에 해당하는 클래스의 대표벡터는 같은 방향이어야하고, 그 외 클래스의 대표벡터는 다른 방향이어야 목적함수 값이 최대화됩니다. Word2Vec (Skip-Gram)에 적용해 보면, \(P(y|x)\)에서 x는 중심단어(target word/center word), y는 주변단어(context word)입니다. 다시 말해 \(P(y|x)\)는 중심단어가 주어졌을 때 주변단어가 등장할 조건부확률을 의미하며, 이 식을 최대화하는 것은 중심단어로 주변단어를 잘 맞춘다는 뜻입니다. 다시 수식의 우변으로 돌아와 분자와 분모를 살펴보겠습니다. 분자를 증가시킨다는 것은 중심단어(x)와 주변단어(y)를 벡터 공간에 놓을 때 주변에 위치시킴으로써 내적값을 크게 만드는 것을 의미하며, 이는 곧 유사도를 높인다고 해석할 수 있습니다. 분모를 줄이기 위해서는 어떻게 해야 할까요? 분모를 줄이기 위해서는 중심단어(x)와 주변에 등장하지 않은 단어(except y)와의 내적값이 작아져야 합니다. 즉 중심단어 주변에 등장하지 않은 단어에 해당하는 벡터와 중심단어 벡터는 벡터 공간에 멀리 떨어지도록 하여 유사도를 줄인다고 해석할 수 있습니다. 

 

다음 포스팅에서는 Word2Vec의 구조와 학습 원리에 대하여 자세히 살펴보고 넘어가겠습니다. 

참고자료

1. Dense Vectors: Capturing Meaning with Code | Pinecone

Dense Vectors: Capturing Meaning with Code | Pinecone

2. https://medium.com/aimonks/from-words-to-vectors-building-a-skip-gram-model-from-scratch-077ed529dcd3

From Words to Vectors: Building a Skip-Gram Model from Scratch

3. Korean Word2Vec

Korean Word2Vec

4. 골든플래닛

GoldenPlanet | 빅데이터 공부 한 걸음: Word2Vec 이란?

5. Word / Document embedding (Word2Vec / Doc2Vec) | LOVIT x DATA SCIENCE

Word / Document embedding (Word2Vec / Doc2Vec)